机器学习基础4-增强学习初探

什么是增强学习
机器学习算法大致可以分为三种:
监督学习(回归,分类)
非监督学习(聚类,降维)
增强学习
增强学习(reinforcement learning, RL)又叫强化学习,增强学习关注的是智能体如何在环境中采取一系列行为,从而获得最大的累积回报。通过增强学习,一个智能体应该知道在什么状态下应该采取什么行动。RL是从环境状态到动作的映射的学习,我们把这个映射称为策略。
增强学习和监督学习的区别主要有以下两点:
增强学习是试错学习(trail-and-error),由于没有直接的指导信息,智能体要不断与环境进行交互,通过试错的方式来获得最佳策略。
延迟回报,增强学习的指导信息很少,而且往往是在事后(最后一个状态)才给出,这就导致了一个问题,就是获得正回报或者负回报以后,如何将回报分配给前面的状态。
马尔可夫决策过程
智能体在环境中的一系列行为可以用马尔可夫决策过程来表示(markov decision process, MDP)。在说马尔可夫决策过程前先说一下,马尔可夫性(无后效性),也就是指系统的下个状态只与当前状态信息有关,而与更早之前的状态无关。马尔可夫决策过程(markov decision process, MDP)也具有马尔可夫性,MDP不仅考虑状态还考虑动作,即系统下个状态不仅和当前状态有关,也和当前采取的动作有关。例如下棋,当我们在某个局面(状态 $s$ )走了一步(动作 $a$ ),这时对手的选择(导致下个状态 $s'$ )我们是不能确定的,但是他的选择只和 $s$ 和 $a$ 有关,而不用考虑更早之前的状态和动作,即 $s'$ 是根据 $s$ 和 $a$ 随机生成的。
一个马尔可夫决策过程由一个四元组构成 $M=(S, A, P_{sa}, R)$
- $S$: 表示状态集合(states),有 $s \in S$ , $s_i$表示第i步的状态。
- $A$: 表示动作集合(actions),有 $a \in A$ , $a_i$表示第i步的动作。
- $P_{sa}$: 表示状态转移概率集合,$P_{sa}$ 表示是在当前 $s \in S$ 状态下,经过 $a \in A$作用后,会转移到其他状态的概率分布情。比如在状态 $s$ 下执行动作 $a$ ,转移到 $s'$ 的概率可以表示为 $p(s'|s, a)$
- $R: S \times A \to \mathbb{R}$,$R$ 是回报函数(reward function),是状态集合 $S$ 和动作集合 $A$ 的积到实数 $\mathbb{R}$ 的映射,表示该状态下该动作的立即回报值,记为 $r(s, a)$ 。
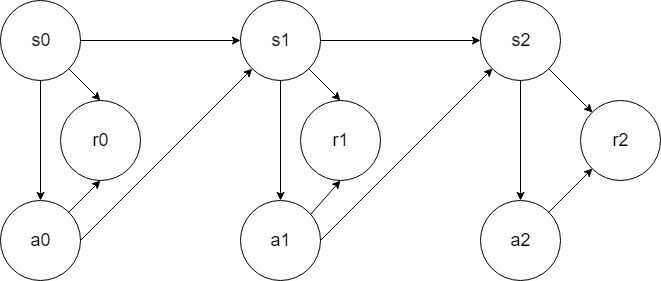
MDP的动态过程如下:某个智能体(agent)的初始化状态为 $s_0$ ,然后从 $A$ 中挑选一个动作 $a_0$ 执行。执行后,agent按 $P_{sa}$概率随机转移到了下一个 $s_1$状态。然后再执行一个动作 $a_1$ ,就转移到了 $s_2$ ,接下来再执行 $a_2$ ...,如下图:
折算累计回报值函数
增强学习学到的是一个从环境状态到动作的映射(即行为策略),记为策略 $\Pi: S \to A$ 。而增强学习往往又具有延迟回报的特点:如果再第 $n$ 步输掉了棋,那么只有状态 $s_n$ 和动作 $a_n$ 获得了立即回报 $r(s_n, a_n)=-1$ ,前面的所有状态立即回报均为0。所以对于之前的任意状态 $s$ 和动作 $a$ ,立即回报函数 $r(s, a)$ 无法说明决策的好坏。因而需要定义值函数(value function)来表明当前状态下策略 $\pi$的长期影响。
当我们遵循某个策略 $\pi$ ,所以有 $a_0=\pi(s_0), a_1=\pi(s_1), a_2=\pi(s_2) \cdots$ ,我们将值函数定义如下: \begin{align} V^\pi(s) & =E[r(s_0, a_0)) + \gamma r(s_1, a_1) + \gamma^2 r(s_2, a_2) + \cdots | s_0=s, \pi] \\ & = E[r(s_0, a_0) + \gamma E[r(s_1, a_1) + \gamma r(s_2, a_2) + \cdots ] | s_0=s, \pi] \\ & = E[r(s, \pi(s)) + \gamma V^\pi(s')] \\ \end{align}
上述式中 $\gamma \in [0, 1]$ 称为折合因子,表明了未来的回报相对于当前回报的重要程度。特别的, $\gamma=0$ 时,相当于只考虑立即回报不考虑长期回报,$\gamma=1$ 时,将长期回报和立即回报看得同等重要。
因为下个时刻将以概率 $p(s'|s, \pi(s))$ 转向下个状态 $s'$ ,所以上式子的期望可以写为: \begin{align} V^\pi(s) &= E[r(s, \pi(s)) + \gamma V^\pi(s')] \\ &= \sum_{s' \in S}p(s'|s, \pi(s))[r(s, \pi(s)) + \gamma V^\pi(s')] \\ &= r(s, \pi(s)) + \gamma \sum_{s' \in S}p(s'|s, \pi(s))V^\pi(s') \\ \end{align}
值函数表明的是当前状态下策略 $\pi$ 的长期影响,也就是说策略 $\pi$ 越好,值函数越大。
我们的目的就是要找一个在任意初始条件 $s$ 下都能最大化值函数的策略,所以MDP的最优策略如下式:
$$\pi^*= arg \ \max_\pi V^\pi(s), (\forall s)$$
动作值函数
上面我们的值函数只与状态 $s$ 有关,我们定义一个和状态,动作都有关的动作值函数,如下: \begin{align} Q^\pi (s, a) &= E[r(s_0, a_0) + \gamma r(s_1, a_1) + \gamma^2 r(s_2, a_2) + \cdots | s_0=s, a_0 = a, \pi] \\ &= E[r(s, a) + \gamma Q^\pi(s', \pi(s'))] \\ &= \sum_{s' \in S}p(s'|s, a)[r(s, a) + \gamma Q^\pi(s', \pi(s'))] \\ &= r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)Q^\pi(s', \pi(s')) \\ \end{align}
很显然 $Q^\pi(s', \pi(s'))$ 即为 $V^\pi(s')$ ,所以有: $$Q^\pi (s, a)=r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)V^\pi(s')$$
动作值函数表明的是当前状态和动作下策略 $\pi$ 的长期影响。那么在指定策略和状态的条件下,不同动作对应的动作值就是代表该动作的价值。
贝尔曼方程
根据值函数和动作值函数我们得到了两个方程: \begin{align} V^\pi(s) &= r(s, \pi(s)) + \gamma \sum_{s' \in S}p(s'|s, \pi(s))V^\pi(s') \\ Q^\pi (s, a) &= r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)V^\pi(s') \\ \end{align}
记最优策略 $ \pi^* $ ,那么 $ \pi^* $ 对应的状态值函数 $V^* (s)$ 和动作值函数 $Q^* (s, a)$ 都为最大化。很容易理解最优的策略 $ \pi^* $ ,就是选择动作值最大的去执行,所以有如下关系:
$$ V^* (s) = \max_a Q^* (s,a) $$
所以得到如下的最优化方程:
$$ V^* (s) = \max_a[r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)V^* (s')] $$
$$ Q^* (s, a) = r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)\max_{a'} Q^* (s',a') $$
策略估计
对于任意的策略 $\pi$ ,我们如何计算其状态值函数 $V^\pi(s)$ ?这个问题就是策略估计。
对于确定性策略,我们有值函数: $$ V^\pi(s) = r(s, \pi(s)) + \gamma \sum_{s' \in S}p(s'|s, \pi(s))V^\pi(s') $$
我们可以使用如下算法进行策略估计:
\begin{align} & Input \ \pi , the \ policy \ to \ be \ evaluated \\ & Initialize \ an \ array \ V(s) = 0, \ for \ all \ s \ \in S \\ & Repeat \\ & \quad \Delta \leftarrow 0 \\ & \quad For \ each \ s \in S: \\ & \quad \quad temp \leftarrow V(s) \\ & \quad \quad V(s) = r(s, \pi(s)) + \gamma \sum_{s' \in S}p(s'|s, \pi(s))V(s') \\ & \quad \quad \Delta \leftarrow \max(\Delta,|temp-V(s)|) \\ & Until \ \Delta < \theta \ (a \ small \ positive \ number) \\ & Output \ V \approx V_\pi \\ \end{align}
策略改进(Policy Improvement)
进行策略估计的目的是为了寻找更好的策略,这个过程叫策略改进(Policy Improvement)。 假设我们有一个策略 $\pi$ ,并且确定了它的所有状态的值函数 $V^\pi(s)$ 。对于某状态 $s$ ,有动作 $a_0=\pi(s)$ 。如果我们在状态 $s$ 下不采取动作 $a_0$ ,而是采用其他动作是否会更好呢?动作值函数 $Q^\pi(s, a)$ 可以来帮助我们进行判断。
评价标准是:$Q^\pi(s,a)$ 是否大于 $V^\pi(s)$ 。如果 $Q^\pi(s,a) > V^\pi(s)$,至少说明新策略[仅在状态 $s$ 下采用动作 $a$ ,其他状态下遵循策略 $\pi$ ]比旧策略[所有状态下都遵循策略 $\pi$ ]整体上要更好。
策略改进定理(policy improvement theorem):$\pi$ 和 $\pi'$ 是两个确定的策略,如果对所有状态 $s\in S $ 有 $Q^\pi(s, \pi'(s)) \ge V^\pi(s)$ ,那么策略 $\pi'$ 必然比策略 $\pi$ 更好,或者至少一样好。其中的不等式等价于 $V^{\pi'}(s) \ge V\pi(s) $ 。
有了改进策略的方法和定理,我们可以遍历所有状态和所有可能的动作 $a$ ,并采用贪心策略来获得新策略 $\pi'$ 。即对所有的 $s \in S$ ,采用下式更新策略:
\begin{align} \pi'(s) &= arg \max_a Q^\pi(s, a) \\ &= arg \max_a [r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)V^\pi(s')] \end{align}
策略迭代(Policy Iteration)
策略迭代就是使用循环进行策略估计和策略改进。假设我们有一个策略 $\pi$ ,那么我们用策略估计获得值函数 $V^\pi(s)$ ,然后根据策略改进得到更好的策略 $\pi'$ ,接着再进行策略估计,再获得更好的策略,整个过程如下:
$$ \pi0 \to V^{\pi0} \to \pi1 \to V^{\pi1} \to \pi2 \to V^{\pi2} \to \cdots \to \pi^* \to V^* $$
这样我们就可以得到一个最优的策略。
完成算法如下:
\begin{align} & 1. \ Initialization \\ & \quad V(s) = 0 \ and \ \pi(s) \in A(s) \ arbitrarily \ for \ all \ s \in S \\ & 2. \ Policy \ Evaluation \\ & \quad Repeat \\ & \quad \quad \Delta \leftarrow 0 \\ & \quad \quad For \ each \ s \in S: \\ & \quad \quad \quad temp \leftarrow V(s) \\ & \quad \quad \quad V(s) \leftarrow r(s, \pi(s)) + \gamma \sum_{s' \in S}p(s'|s, \pi(s))V(s') \\ & \quad \quad \quad \Delta \leftarrow \max(\Delta, |temp-V(s)|) \\ & \quad Until \ \Delta < \theta \ (a \ small \ positive \ number) \\ & 3. \ Policy \ Improvement \\ & \quad policy-stable \leftarrow true \\ & \quad For \ each \ s \in S: \\ & \quad \quad temp \leftarrow \pi(s) \\ & \quad \quad \pi(s) \leftarrow arg \max_a [r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a)V^\pi(s')] \\ & \quad \quad If \ temp \neq \pi(s), \ then \ policy-stable \leftarrow false \\ & \quad If \ policy-table, \ then \ stop \ and \ return \ V \ and \ \pi; \ else \ go \ to \ 2 \\ \end{align}
值迭代(Value Iteration)
策略迭代算法包含策略估计,策略估计需要循环扫描所有状态很多次,计算量比较大。值迭代可以保证算法收敛的情况下,缩短策略估计的过程。值迭代对所有的 $s\in S$ 按照下列公式更新:
$$ V(s)=\max_a[r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a) V(s')] $$
值迭代完整算法如下: \begin{align} & Initialize \ array \ V \ arbitrarily \ (e.g., \ V(s)=0 \ for \ all \ s \in S) \\ & Repeat \\ & \quad \Delta \leftarrow 0 \\ & \quad For \ each \ s \in S: \\ & \quad \quad temp \leftarrow V(s) \\ & \quad \quad V(s) \leftarrow \max_a[r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a) V(s')] \\ & \quad \quad \Delta \leftarrow max(\Delta, |temp-V(s)|) \\ & Until \ \Delta < \theta \ (a \ small \ positive \ number) \\ & \\ & Output \ a \ deterministic \ policy, \ \pi , \ such \ that \\ & \quad \pi(s) = arg \max_a[r(s, a) + \gamma \sum_{s' \in S}p(s'|s, a) V(s')] \\ \end{align}
值迭代可以理解成采用迭代的方式逼近贝尔曼最优方程。
策略迭代和值迭代都要求一个完全已知的环境模型(状态转移概率 $p(s'|s, a)$)。
蒙特卡罗方法
蒙特卡罗方法又叫统计模拟方法,蒙特卡罗方法不要求一个完全已知的环境模型(状态转移概率 $p(s'|s, a)$)。蒙特卡罗法通过经验就可以求得最优策略,经验就是训练样本,比如在初始状态 $s$ 下,遵循策略 $\pi$ ,最终得到了总回报 $R$ ,这就是一个样本。蒙特卡罗法是定义在episode task上的,也就是不管采取什么策略,都会在有限时间内达到终止状态并获得回报。一个样本也就是一个episode。
蒙特卡罗策略估计
假设我们在策略 $\pi$ 下得到了一些episode,那么我们如何估计某个状态 $s$ 的 $V^\pi(s)$ ?一个明显的方法是我们找出达到过状态 $s$ 的episode,然后取这些episode回报的平均值。当经过无穷多的episode后, $V^\pi(s)$ 的估计值将收敛到真实值。
蒙特卡罗动作值估计
在策略估计后,我们得到各个状态的状态值,但是因为没有状态转移概率 $p(s'|s, a)$ ,所以我们无法进行策略改进。实际上我们可以直接进行动作值估计,假设我们要估计 $Q^\pi(s, a)$ 的值,那么我们可以找出在状态 $s$ 下执行过动作 $a$ 的episode,然后然后取这些episode回报的平均值,就是我们的估计值。得到了动作值,就可以进行策略改进: $\pi'(s) = arg \max_a Q^\pi(s, a)$ 。
蒙特卡罗策略迭代
实际上我们可以每进行一个episode就重新计算episode中每对 $(s, a)$ 对应的动作值,并进行策略改进,这种方式类似于随机梯度下降,当然在一个episode中我们只会计算第一次出现的$(s, a)$。完整算法如下:
\begin{align} & Initialize, \ for \ all \ s \in S, \ a \in A(s): \\ & \quad Q(s, a) \leftarrow 0 \\ & \quad \pi(s) \leftarrow arbitrary \\ & \quad n=0 \\ & Repeat \ forever: \\ & \quad (a) \ Choose \ s_0 \in S \ and \ a_0 \in A(s_0), \ \\ & \quad \quad \ \ Generate \ an \ episode \ starting \ from s_0,a_0, \ following \ \pi \\ & \quad \quad \ \ n \leftarrow n+1 \\ & \quad (b) \ For \ each \ different \ pair \ s, a \ appearing \ in \ the \ episode: \\ & \quad \quad \ \ \quad Q(s,a) \leftarrow {Q(s,a) * (n-1) + r \over n} \\ & \quad (c) \ For \ each \ defferent \ s \ in \ the \ episode: \\ & \quad \quad \ \ \quad \pi(s) \leftarrow arg \max_aQ(s,a) \\ \end{align}
以上的算法还存在一个问题,假设在某个确定状态 $s_0$ 下,能执行 $a_0, a_1, a_2$这三个动作。如果智能体已经估计了 $Q(s_0, a_0), Q(s_0, a_1)$ ,并且 $Q(s_0, a_0) > Q(s_0, a_1)$,那么它在未来只会执行 $a_0$ 这个动作,导致无法更新 $Q(s_0, a_1), Q(s_0, a_2)$ ,然而我们并不能保证 $Q(s_0, a_0)$就是 $s_0$下最大的动作值。对于这个问题可以用soft policies来解决,比如 $\epsilon - gerrdy \ policy$ ,即在所有状态下,用 $1-\epsilon$ 的概率来执行当前的最优动作, $\epsilon$的概率来执行其他动作,通过慢慢减少 $\epsilon$ 的值,最终使算法收敛。
Q-Learning
只要能我们计算出所有的动作值,也就找到了最优策略 $ \pi^* $,动作值可以用矩阵表示(Q-Table): $$ \begin{array} {c|ccc} \ & a_0 & a_1 & a_2 \\ \hline s_0 & Q(0, 0) & Q(0, 1) & Q(0, 2) \\ s_1 & Q(1, 0) & Q(1, 1) & Q(1, 2) \\ s_2 & Q(2, 0) & Q(2, 1) & Q(2, 2) \\ \end{array} $$ 蒙特卡罗策略迭代要求一个完整的episode才可以更新Q-Table,我们可以采用时间差分法更新Q-Table,该方法不要求已知的环境模型,并且是单步更新(不要求完整的episode),更新公式如下: $$ Q(s, a) \leftarrow Q(s,a)+\alpha[r(s,a)+\gamma\max_{a'}Q(s',a')-Q(s,a)] $$ 上述式中 $\alpha$ 为学习速度,完整算法如下:
\begin{align} & Initialize \ Q(s,a) \ arbitrarily \\ & Repeat \ (for \ each \ episode): \\ & \quad Initialize \ s \\ & \quad Repeat \ (for \ each \ step \ of \ episode): \\ & \quad \quad Choose \ a \ from \ s \ using \ policy \ derived \ from \ Q \ (e.g., \ \epsilon - gerrdy) \\ & \quad \quad Take \ action \ a, \ observe \ r(s,a), \ s' \\ & \quad \quad Q(s, a) \leftarrow Q(s,a)+\alpha[r(s,a)+\gamma\max_{a'}Q(s',a')-Q(s,a)] \\ & \quad \quad s \leftarrow s' \\ & \quad until \ s \ is \ terminal \\ \end{align}
其他章节链接
机器学习基础4-增强学习初探







还没有人评论...