机器学习基础1-线性回归及C++实现
回归问题
给定多个自变量,一个因变量以及代表它们之间关系的一些训练样本,如何来确定它们之间的关系。
线性模型
设自变量的个数即特征数量为 $n$ 即,自变量为 $x$ ,自变量的参数为 $\theta$ ,我们定义它们的关系如下:
\begin{align} h_\theta(x) & = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n \\ & = x\theta \\ \\ \theta & = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix} \\ \\ x & = \begin{bmatrix} 1 \ x_1 \ \cdots \ x_n \end{bmatrix} \\ \end{align}
设训练样本数为 $m$,训练样本集为 $X$ ,训练输出集为 $Y$ ,如下: \begin{align} X & = \begin{bmatrix} x^{0} \\ x^{1} \\ \cdots \\ x^{m-1} \end{bmatrix} \\ \\ Y & = \begin{bmatrix} y^{0} \\ y^{1} \\ \vdots \\ y^{m-1} \end{bmatrix} \\ \end{align}
我们的目标是已知 $X$ 和 $Y$ 的情况下得到最优的 $\theta$。
损失函数
哪个 $\theta$ 是最优的?我们需要先定义损失函数: $$ J(\theta)=\frac{1}{2}\sum_{i=0}^{m-1}(h_\theta(x^i)-y^i)^2 $$ 很明显损失函数最小值对应的 $\theta$ 就是我们求解的目标,所以问题变为: $$ \min_\theta J_\theta $$
梯度下降法
使用梯度下降法可以帮助我们找到损失函数的最小值,参数 $\theta_j$的梯度为:
$$ \frac{\partial J(\theta)}{\partial \theta_j}=\frac{\partial}{\partial \theta_j} \frac{1}{2}\sum_{i=0}^{m-1}(h_\theta(x^i)-y^i)^2 $$
假设样本数为1,则得到如下: $$ \frac{\partial J(\theta)}{\partial \theta_j}=\frac{\partial}{\partial \theta_j} \frac{1}{2}(h_\theta(x)-y)^2 $$
$$ \frac{\partial J(\theta)}{\partial \theta_j}=(h_\theta(x)-y)\frac{\partial}{\partial \theta_j}(h_\theta(x)-y) $$
$$ \frac{\partial J(\theta)}{\partial \theta_j}=(h_\theta(x)-y)x_j $$
多个样本的正确公式如下: $$ \frac{\partial J(\theta)}{\partial \theta_j}=\sum_{i=0}^{m-1}((h_\theta(x^i)-y^i)x_j^i) $$
$\theta_j$的更新公式为:($\alpha$ 为学习速度) $$ \theta_j := \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j} $$
$$ \theta_j := \theta_j - \alpha \sum_{i=0}^{m-1}((h_\theta(x^i)-y^i)x_j^i) $$
等价的矩阵形式更新公式为: $$ \theta := \theta - X^T \cdot (X \cdot \theta-Y) \cdot \alpha $$
随机梯度和批量梯度
如果我们每次更新 $\theta$ 都使用所有的训练样本,在训练样本总量很大的情况下可能会耗费很多的资源,虽然这样训练的效果会很好。
我们也可以每次只选择一个训练样本来进行更新,这就是随机梯度下降法,相比于梯度下降法随机梯度下降法可能收敛较慢。
除此之外我们也可以选择部分训练样本来更新,用以平衡收敛速度和耗费资源的情况,这种方式称为批量梯度下降。
学习速度
在公式中我们还看到一个学习速度的参数 $\alpha$ ,该值需要取正数。如果该值设置很小会导致收敛速度很慢,如果设置很大会导致在最优点左右震荡。
C++代码实现
我们定义如下的接口:
typedef LMatrix<float> LRegressionMatrix;
class CLinearRegression;
/// @brief 线性回归类
class LLinearRegression
{
public:
/// @brief 构造函数
LLinearRegression();
/// @brief 析构函数
~LLinearRegression();
/// @brief 训练模型
/// 如果一次训练的样本数量为1, 则为随机梯度下降
/// 如果一次训练的样本数量为M(样本总数), 则为梯度下降
/// 如果一次训练的样本数量为m(1 < m < M), 则为批量梯度下降
/// @param[in] xMatrix 样本矩阵, 每一行代表一个样本, 每一列代表样本的一个特征
/// @param[in] yVector(列向量) 样本输出向量, 每一行代表一个样本
/// @param[in] alpha 学习速度, 该值必须大于0.0f
/// @return 成功返回true, 失败返回false(参数错误的情况下会返回失败)
bool TrainModel(IN const LRegressionMatrix& xMatrix, IN const LRegressionMatrix& yVector, IN float alpha);
/// @brief 使用训练好的模型预测数据
/// @param[in] xMatrix 需要预测的样本矩阵
/// @param[out] yVector 存储预测的结果向量(列向量)
/// @return 成功返回true, 失败返回false(模型未训练或参数错误的情况下会返回失败)
bool Predict(IN const LRegressionMatrix& xMatrix, OUT LRegressionMatrix& yVector) const;
/// @brief 计算损失值, 损失值为大于等于0的数, 损失值越小模型越好
/// @param[in] xMatrix 样本矩阵, 每一行代表一个样本, 每一列代表样本的一个特征
/// @param[in] yVector(列向量) 样本输出向量, 每一行代表一个样本
/// @return 成功返回损失值, 失败返回-1.0f(参数错误的情况下会返回失败)
float LossValue(IN const LRegressionMatrix& xMatrix, IN const LRegressionMatrix& yVector) const;
private:
CLinearRegression* m_pLinearRegression; ///< 线性回归实现对象
};
LMatrix是我们自定义的矩阵类,用于方便机器学习的一些矩阵计算,关于它的详细代码可以查看链接:猛戳我
我们为LLinearRegression设计了三个方法TrainModel,Predict以及LossValue,用于训练模型,预测新数据以及计算损失值。
我们看一下TrainModel的实现:
LRegressionMatrix X;
Regression::SamplexAddConstant(xMatrix, X);
const LRegressionMatrix& Y = yVector;
LRegressionMatrix& W = m_wVector;
LRegressionMatrix XT = X.T();
LRegressionMatrix XW;
LRegressionMatrix DW;
/*
h(x) = X * W
wj = wj - α * ∑((h(x)-y) * xj)
*/
LRegressionMatrix::MUL(X, W, XW);
LRegressionMatrix::SUB(XW, Y, XW);
LRegressionMatrix::MUL(XT, XW, DW);
LRegressionMatrix::SCALARMUL(DW, -1.0f * alpha, DW);
LRegressionMatrix::ADD(W, DW, W);
在代码中我们给样本数据最后一列加上一个常数项1.0,之后就根据上面的矩阵公式更新参数。
我们再看一下Predict的实现:
LRegressionMatrix X;
Regression::SamplexAddConstant(xMatrix, X);
LRegressionMatrix::MUL(X, m_wVector, yVector);
我们只要在样本最后一列增加一个常数项,将样本矩阵乘以参数(权重)向量就得到预测结果。
下面我们来测试一下我们的线性回归算法:
int main()
{
// 定义训练样本
float trainX[4] =
{
2.0f,
4.0f,
6.0f,
8.0f
};
LRegressionMatrix xMatrix(4, 1, trainX);
// 定义训练样本输出
float trainY[4] =
{
1.0f,
2.0f,
3.0f,
4.0f
};
LRegressionMatrix yMatrix(4, 1, trainY);
// 定义线性回归对象
LLinearRegression linearReg;
// 训练模型
// 计算每一次训练后的损失值
for (unsigned int i = 0; i < 10; i++)
{
linearReg.TrainModel(xMatrix, yMatrix, 0.01f);
float loss = linearReg.LossValue(xMatrix, yMatrix);
printf("Train Time: %u ", i);
printf("Loss Value: %f\n", loss);
}
// 进行预测
LRegressionMatrix yVector;
linearReg.Predict(xMatrix, yVector);
printf("Predict Value: ");
for (unsigned int i = 0; i < yVector.RowLen; i++)
{
printf("%.5f ", yVector[i][0]);
}
printf("\n");
system("pause");
return 0;
}
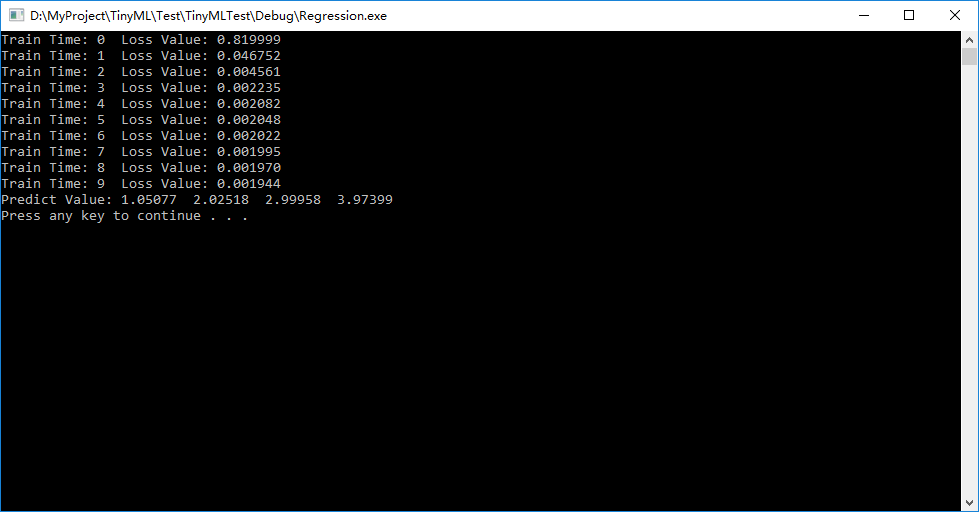
我们得到如下结果:
我们看到随着训练次数的增多损失值一直在减小,并且我们预测的结果也很贴近正确结果。
局部加权回归
线性回归要求数据是线性的,针对非线性数据我们可以使用局部加权回归方法,非线性数据在局部可能是线性的。我们需要定义如下的损失函数:
$$ J(\theta)=\frac{1}{2}\sum_{i=0}^{m-1}k_i(h_\theta(x^i)-y^i)^2 $$
$$ k_i=e^{-\frac{(x^i-x^t)^2}{2}} $$
我们看到公式中有一个 $x^t$ ,它代表我们想要预测的目标点,$(x^i-x^t)^2$ 为两点之间的距离,从公式中可以看出远离我们目标点的训练数据占的权重会比较小,该损失函数会更在意靠近我们目标点的训练数据。
以上完整的代码可以在链接:猛戳我查看,我们的线性回归被定义在文件LRegression.h和LRegression.cpp中。
其他章节链接
机器学习基础1-线性回归及C++实现







还没有人评论...