机器学习基础2-二项逻辑回归及C++实现

分类问题
生活中我们会遇到很多分类问题,如一封邮件是否是垃圾邮件等。那么能否建立一种模型来给出垃圾邮件的概率?通过前面线性回归一文我们知道线性回归的结果是一个连续值,并且它的范围是无法限定的,而分类问题需要我们给出一个0.0~1.0之间的概率值,那么有没有什么办法可以将线性回归的结果值映射为一个0.0~1.0之间的概率值呢?有!它就是逻辑函数。
逻辑函数是一种S函数,函数形式为:
$$ p(t)=\frac{1}{1+e^{-t}} $$
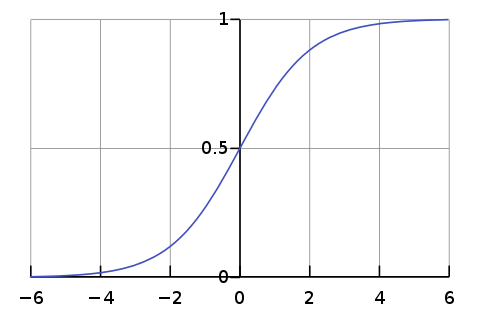
逻辑函数的函数图像为(来源于维基百科):
二项逻辑回归模型
利用逻辑函数我们可以构造二项逻辑回归模型(binomial logistic regression model)。二项逻辑回归模型中的二项意为二分类,也就是分类类别 $y\in{0,1}$ 。
设特征数量为 $n$ 即,特征为 $x$ ,特征的参数为 $\theta$ ,我们定义如下:
\begin{align} \\ x & = \begin{bmatrix} 1 \ x_1 \ \cdots \ x_n \end{bmatrix} \\ \\ \theta & = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix} \\ \\ x\theta & = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n \\ \\ h_\theta(x) & = \frac{1}{1+e^{x\theta}} \end{align}
$h_\theta(x)$ 就是我们的概率函数,我们可以假设它为分类类别为1的概率,那么类别1和类别0的概率分别为:
\begin{align} \\ P(y=1 \mid x) & =h_\theta(x) \\ \\ P(y=0 \mid x) & =1-h_\theta(x) \\ \end{align}
综合起来可以写成: \begin{align} \\ P(y \mid x) & =h_\theta(x)^y(1-h_\theta(x))^{1-y} \\ \end{align}
设训练样本数为 $m$,训练样本集为 $X$ ,训练输出集为 $Y$ ,如下: \begin{align} X & = \begin{bmatrix} x^{0} \\ x^{1} \\ \cdots \\ x^{m-1} \end{bmatrix} \\ \\ Y & = \begin{bmatrix} y^{0} \\ y^{1} \\ \vdots \\ y^{m-1} \end{bmatrix} \\ \end{align}
我们的目标是已知 $X$ 和 $Y$ 的情况下得到最优的 $\theta$。
似然函数
哪个 $\theta$ 是最优的?我们需要先定义似然函数:
\begin{align} \\ L(\theta) &= \prod_{i=0}^{m-1} P(y^i \mid x^i) \\ \\ L(\theta) &= \prod_{i=0}^{m-1}h_\theta(x^i)^{y^i} (1-h_\theta(x^i))^{1-y^i} \\ \end{align}
我们在似然函数中引入自然对数以方便后续的求导,则:
\begin{align} \\ L(\theta) &= \log(\prod_{i=0}^{m-1}h_\theta(x^i)^{y^i} (1-h_\theta(x^i))^{1-y^i}) \\ L(\theta) &= \sum_{i=0}^{m-1}\log(h_\theta(x^i)^{y^i} (1-h_\theta(x^i))^{1-y^i}) \\ L(\theta) &= \sum_{i=0}^{m-1}(y^i\log(h_\theta(x^i)) + (1-y^i)\log(1-h_\theta(x^i))) \\ \end{align}
很明显似然函数最大值对应的 $\theta$ 就是我们求解的目标,所以问题变为: $$ \max_\theta L_\theta $$
梯度上升法
使用梯度上升法可以帮助我们找到似然函数的最大值,参数 $\theta_j$的梯度为:
$$ \frac{\partial L(\theta)}{\partial \theta_j}=\frac{\partial}{\partial \theta_j} \sum_{i=0}^{m-1}(y^i\log(h_\theta(x^i)) + (1-y^i)\log(1-h_\theta(x^i))) $$
假设样本数为1,则得到如下: \begin{align} \\ \frac{\partial L(\theta)}{\partial \theta_j} &= \frac{\partial}{\partial \theta_j} (y\log(h_\theta(x)) + (1-y)\log(1-h_\theta(x))) \\ \\ \frac{\partial L(\theta)}{\partial \theta_j} &= \frac{y}{h_\theta(x)} \frac{\partial}{\partial \theta_j} h_\theta(x) + \frac{1-y}{1-h_\theta(x)}\frac{\partial}{\partial \theta_j}(1-h_\theta(x)) \\ \\ \frac{\partial L(\theta)}{\partial \theta_j} &= (\frac{y}{h_\theta(x)} - \frac{1-y}{1-h_\theta(x)})\frac{\partial}{\partial \theta_j} h_\theta(x) \\ \end{align}
又因为:
\begin{align} \\ \frac{\partial}{\partial \theta_j} h_\theta(x) &= \frac{\partial}{\partial \theta_j} \frac{1}{1+e^{x\theta}} \\ \\ \frac{\partial}{\partial \theta_j} h_\theta(x) &=\frac{-1}{(1+e^{x\theta})^2} \frac{\partial}{\partial \theta_j}e^{x\theta} \\ \\ \frac{\partial}{\partial \theta_j} h_\theta(x) &=\frac{-e^{x\theta}}{(1+e^{x\theta})^2} \frac{\partial}{\partial \theta_j} x\theta \\ \\ \frac{\partial}{\partial \theta_j} h_\theta(x) &=-h_\theta(x)(1-h_\theta(x)) \frac{\partial}{\partial \theta_j} x\theta \\ \\ \frac{\partial}{\partial \theta_j} h_\theta(x) &=-h_\theta(x)(1-h_\theta(x)) x_j \\ \end{align}
所以:
\begin{align} \\ \frac{\partial L(\theta)}{\partial \theta_j} &= (\frac{y}{h_\theta(x)} - \frac{1-y}{1-h_\theta(x)})(-h_\theta(x)(1-h_\theta(x)) x_j) \\ \\ \frac{\partial L(\theta)}{\partial \theta_j} &= -(y(1-h_\theta(x)) - (1-y)h_\theta(x))x_j \\ \\ \frac{\partial L(\theta)}{\partial \theta_j} &= -(y-h_\theta(x))x_j \\ \end{align}
多个样本的正确公式为: \begin{align} \\ \frac{\partial L(\theta)}{\partial \theta_j} &= -\sum_{i=0}^{m-1} (y^i-h_\theta(x^i))x_j^i \\ \end{align}
梯度上升法下的 $\theta_j$ 的更新公式为:($\alpha$ 为学习速度)
\begin{align} \\ \theta_j &:= \theta_j + \alpha \frac{\partial L(\theta)}{\partial \theta_j} \\ \\ \theta_j &:= \theta_j - \alpha \sum_{i=0}^{m-1} (y^i-h_\theta(x^i))x_j^i \\ \end{align}
关于随机梯度,批量梯度以及学习速度在上一文线性回归中我们已经介绍过,所以这边不再解释。
C++代码实现
我们定义如下的接口:
typedef LMatrix<float> LRegressionMatrix;
/// @brief 回归中的ZERO分类
#ifndef REGRESSION_ZERO
#define REGRESSION_ZERO 0.0f
#endif
/// @brief 回归中的ONE分类
#ifndef REGRESSION_ONE
#define REGRESSION_ONE 1.0f
#endif
/// @brief 逻辑回归(分类)
class LLogisticRegression
{
public:
/// @brief 构造函数
LLogisticRegression();
/// @brief 析构函数
~LLogisticRegression();
/// @brief 训练模型
/// 如果一次训练的样本数量为1, 则为随机梯度下降
/// 如果一次训练的样本数量为M(样本总数), 则为梯度下降
/// 如果一次训练的样本数量为m(1 < m < M), 则为批量梯度下降
/// @param[in] xMatrix 样本矩阵, 每一行代表一个样本, 每一列代表样本的一个特征
/// @param[in] yVector(列向量) 样本标记向量, 每一行代表一个样本, 值只能为REGRESSION_ONE或REGRESSION_ZERO
/// @param[in] alpha 学习速度, 该值必须大于0.0f
/// @return 成功返回true, 失败返回false(参数错误的情况下会返回失败)
bool TrainModel(IN const LRegressionMatrix& xMatrix, IN const LRegressionMatrix& yVector, IN float alpha);
/// @brief 使用训练好的模型预测数据
/// @param[in] xMatrix 需要预测的样本矩阵
/// @param[out] yVector 存储预测的结果向量(列向量), 值为REGRESSION_ONE标记的概率
/// @return 成功返回true, 失败返回false(模型未训练或参数错误的情况下会返回失败)
bool Predict(IN const LRegressionMatrix& xMatrix, OUT LRegressionMatrix& yVector) const;
/// @brief 计算似然值, 似然值为0.0~1.0之间的数, 似然值值越大模型越好
/// @param[in] xMatrix 样本矩阵, 每一行代表一个样本, 每一列代表样本的一个特征
/// @param[in] yVector(列向量) 样本输出向量, 每一行代表一个样本, 值只能为REGRESSION_ONE或REGRESSION_ZERO
/// @return 成功返回似然值, 失败返回-1.0f(参数错误的情况下会返回失败)
float LikelihoodValue(IN const LRegressionMatrix& xMatrix, IN const LRegressionMatrix& yVector) const;
private:
CLogisticRegression* m_pLogisticRegression; ///< 逻辑回归实现类
};
LMatrix是我们自定义的矩阵类,用于方便机器学习的一些矩阵计算,关于它的详细代码可以查看链接:猛戳我
我们为LLogisticRegression设计了三个方法TrainModel,Predict以及LikelihoodValue,用于训练模型,预测新数据以及计算似然值。
我们看一下TrainModel的实现:
LRegressionMatrix X;
Regression::SamplexAddConstant(xMatrix, X);
const LRegressionMatrix& Y = yVector;
LRegressionMatrix& W = m_wVector;
LRegressionMatrix XT = X.T();
/*
如果h(x) = 1/(1 + e^(X * W)) 则
wj = wj - α * ∑((y - h(x)) * xj)
如果h(x) = 1/(1 + e^(-X * W)) 则
wj = wj + α * ∑((y - h(x)) * xj)
*/
LRegressionMatrix XW(X.RowLen, 1);
LRegressionMatrix DW;
LRegressionMatrix::MUL(X, W, XW);
for (unsigned int m = 0; m < XW.RowLen; m++)
{
this->Sigmoid(XW[m][0], XW[m][0]);
}
LRegressionMatrix::SUB(Y, XW, XW);
LRegressionMatrix::MUL(XT, XW, DW);
LRegressionMatrix::SCALARMUL(DW, -1.0f * alpha, DW);
LRegressionMatrix::ADD(W, DW, W);
逻辑函数定义如下:
/// @brief S型函数
/// @param[in] input 输入值
/// @param[out] output 存储输出值
void Sigmoid(float input, float& output) const
{
output = 1.0f/(1.0f + exp(input));
}
我们看一下Predict的实现:
LRegressionMatrix X;
Regression::SamplexAddConstant(xMatrix, X);
yVector.Reset(X.RowLen, 1, 0.0f);
LRegressionMatrix::MUL(X, m_wVector, yVector);
for (unsigned int m = 0; m < yVector.RowLen; m++)
{
this->Sigmoid(yVector[m][0], yVector[m][0]);
}
最后就是LikelihoodValue的实现:
LRegressionMatrix predictY;
this->Predict(xMatrix, predictY);
float likelihood = 1.0f;
for (unsigned int i = 0; i < yVector.RowLen; i++)
{
if (yVector[i][0] == REGRESSION_ONE)
likelihood *= predictY[i][0];
else if (yVector[i][0] == REGRESSION_ZERO)
likelihood *= (1.0f - predictY[i][0]);
else
return -1.0f;
}
return likelihood;
以上完整的代码可以在链接:猛戳我查看,我们的逻辑回归被定义在文件LRegression.h和LRegression.cpp中。
其他章节链接
机器学习基础2-二项逻辑回归及C++实现







strutsjava4560
发表于: 2017年12月19日
公式排版有误?
burnell liu (作者)
发表于: 2017年12月21日
求教哪里有误